Meshing with Voronoi Polygons

Considerations for a GFM to Voronoi generator to Modeling:

What are constraints on input?
i. single material: piecewise linear complex (triangle) bounding airtight volumes
ii. multi-material: coincident piecewise linear complexes (triangle) bounding multiple airtight volumes

What type of output are possible?
Material properties
Boundary conditions
Variable resolution, High aspect ratio geometry, anisotropic meshing, Non-manifold geometries

Visualization of results?
Output Voronoi polygons, Generator seeds, Paraview (or other?)

Examples

3D Single Material Box 

Directory: /project/ep_cr/tam/meshing/Examples/proto_vor_tet/
Input Surface
VoroCrust Cells (wire) and
Connected Tets (blue and red)
LaGriT Finite Element Mesh 		Interior seeds (red)
Surface constraining seeds (blue)
LaGriT Finite Element Mesh 		VoroCrust Voronoi Polygons
LaGriT Finite Element Mesh 		VoroCrust Voronoi Polygons Clipped
LaGriT Finite Element Mesh

Images show VoroCrust meshing results.
Input is a triangulated surface representing the volume to fill. VC will generate seed points (voronoi centers). These are interior (with voronoi cells full inside) and surface constraining (inside and outside the surface).
The result is a volume filled with voronoi polygons with variable number of faces. VC creates many surface seeds which may be difficult to view and evaluate.
Note, Input models assume vornoi cells around each node point formed from tetrahedral.

3D 2 Materials 

Directory: /project/ep_cr/tam/meshing/Examples/simple_tests/flat_1bndry
Input Surface with 2 Materials
 vc_surface
 vc_surface_with_opacity


2D Single Material Wave Top with Distribution Options

Directory: /project/ep_cr/tam/meshing/Examples/simple_tests/2D_1mat_wave
Input Surface
SP2D_1mat_quin_h20_wave175
 SP2D_1mat_quin_h30_wave175
 SP2D_1mat_rand_h20_wave175
 SP2D_1mat_reg_h20_wave175


PROTO1 2D 4 Corner Points

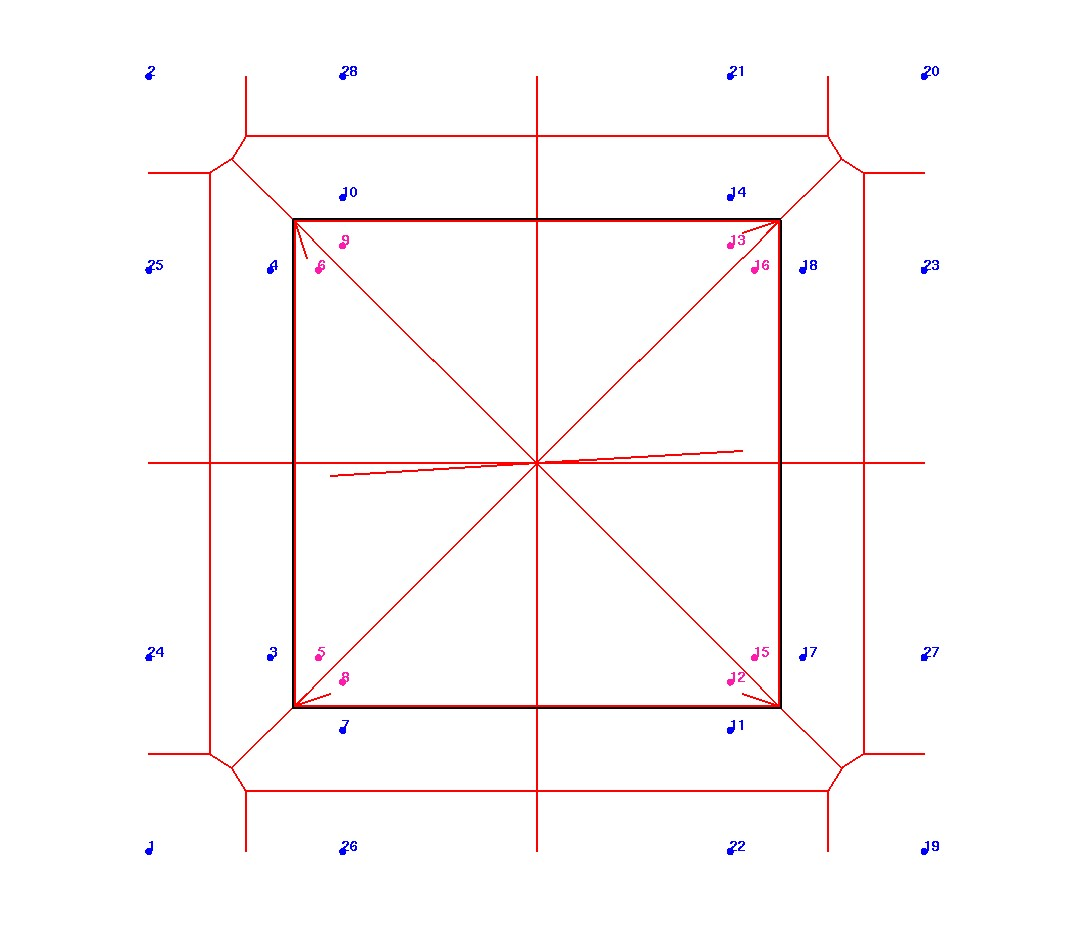
To better understand VC output we create a simplified 2D cube with possible seed locations.
Each corner has 4 seeds located inside and outside of the boundary surface.
The seed points into a Delaunay mesh and Voronoi volumes and areas are computed using LaGriT.


Page for PROTO1 2D Box