The quality of polygons are not good. Some are very small, and some are large.
In order to generate a random spatial point process, one common approach is to use the Poisson Point Process (PPP). Our domain in this case is a square (2D), as we are only concerned with modeling the polygonal pattern appearing on the surface of Arctic land at this point.
Generating a 2D PPP is straightforward. For a realization of N points in a square domain, one can simply use a random number generator to generate random numbers, then translate these number into X-Y coordinates, and distribute the points with these coordinates within the specified domain, until N number of points is reached. In fact, in modeling Arctic polygonal tundra, this method has been introduced in a paper called "A stochastic model for the polygonal tundra based on Poisson-Voronoi Diagrams."[1]
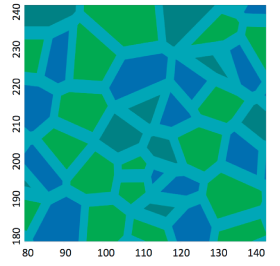
Although using this approach, the eventual polygonal pattern can capture some basic statistics of the Arctic polygons, such as area distribution, it is not appropriate for a full physical model, as it tends to produce bad quality (from mesh generation point of view high aspect ratio, short edges) polygons, resulting from points being generated too closed to each other (Figure. 1).
Moreover, compared to the the actual pattern of Arctic polygons, the Poisson-Voronoi diagrams do not look similar qualitatively. See Figure. 2.
 |
 |
In order to improve the quality of the polygons, as well as achieving a more or less uniform pattern, we generate the points based on a random Poisson-disk Sampling. Similar to the PPP, the Poisson-disk Sampling generates the points randomly, but ensures that the points are at least a distance d apart from each other (Figure. 3).
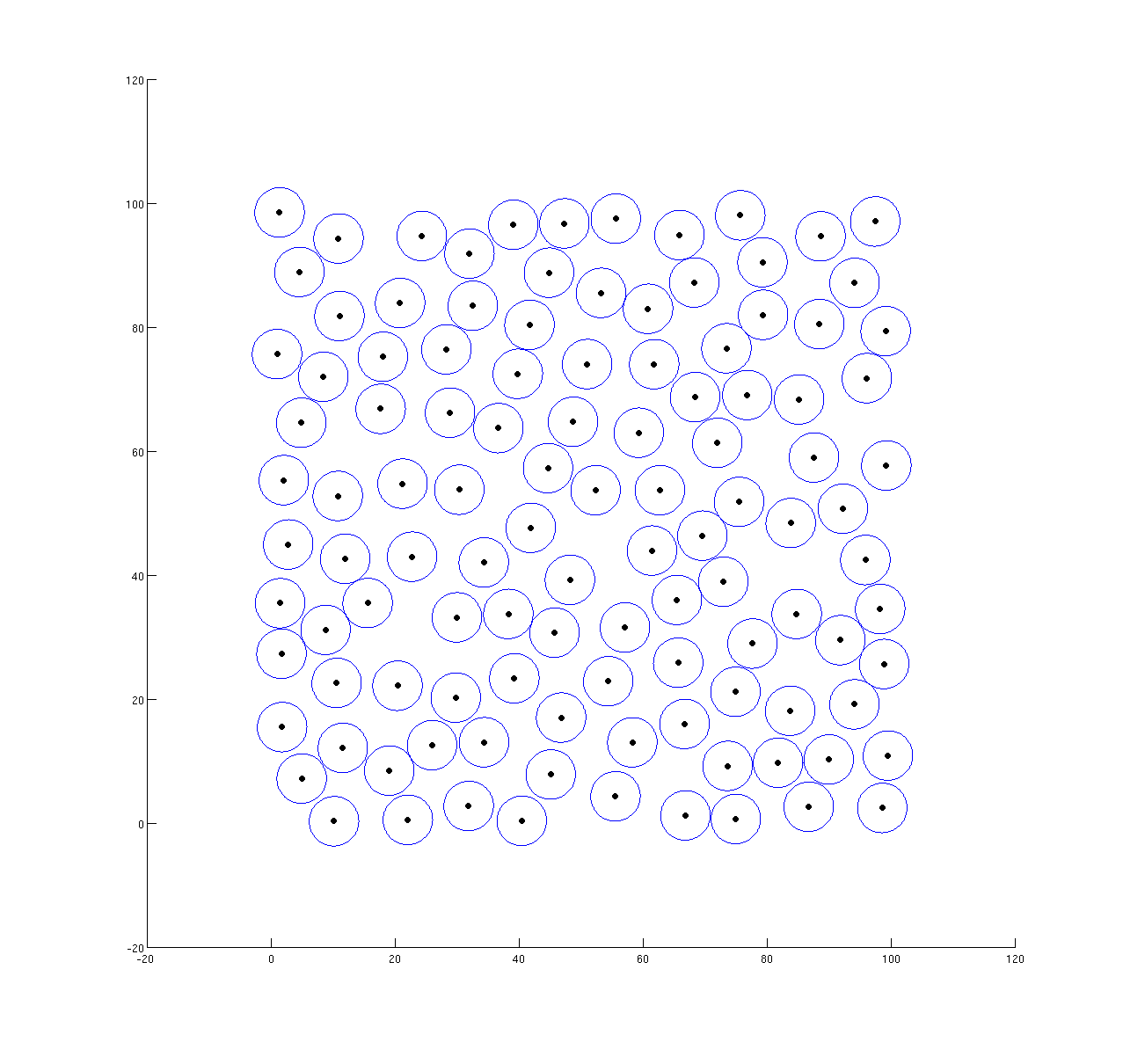 |
1. A stochastic model for the polygonal tundra based on Poisson-Voronoi Diagrams, Earth System Dynamics Discussion, 3, 453-483, 2012. Link